Posterior Inference using SBI

Simulation-Based Inference (SBI) with Neural Posterior Estimation (NPE) is a statistical framework for parameter inference in complex models. Instead of relying on an explicit likelihood function, NPE uses simulations to generate synthetic data and trains neural networks to learn an approximate posterior distribution of the parameters given observed data. This approach is typically used when the likelihood is intractable or expensive to compute, making traditional methods impractical. For pulse profile modelling, while the likelihood computation is tractable, sampling complex high-dimensioinal parameter spaces can get computationally expensive. SBI provides a potentially lucrative alternative to this problem.

In this example notebook, we utilize the sbi package to perform this. Refer to the installation instructions for additional dependencies required to run this notebook.

Initialization

## IMPORTANT: Import sequence - torch, sbi, and xpsi.
import torch
import torch.nn as nn
import torch.nn.functional as F

from sbi import utils as utils
from sbi import analysis as analysis
from sbi.neural_nets import posterior_nn
from sbi.inference import SNPE, simulate_for_sbi
from sbi.utils.user_input_checks import prepare_for_sbi

import numpy as np
import math

from matplotlib import pyplot as plt
from matplotlib import rcParams
rc = {"font.family" : "serif",
      "mathtext.fontset" : "stix"}
plt.rcParams.update(rc)
plt.rcParams["font.serif"] = ["Times New Roman"] + plt.rcParams["font.serif"]
plt.rcParams.update({'font.size': 18})
plt.rcParams.update({'legend.fontsize': 15})

import xpsi

import sys
## Add your path to the example modules to run this notebook
sys.path.append('../../examples/examples_fast/Modules/')


import xpsi.SBI_wrapper as SBI_wrapper
from xpsi.SBI_wrapper import xpsi_wrappers
import xpsi.utilities.Example_CNNs as CNNs

/=============================================\
| X-PSI: X-ray Pulse Simulation and Inference |
|---------------------------------------------|
|                Version: 3.0.0               |
|---------------------------------------------|
|      https://xpsi-group.github.io/xpsi      |
\=============================================/

Imported emcee version: 3.1.6
Imported PyMultiNest.
Imported UltraNest.
Imported GetDist version: 1.5.3
Imported nestcheck version: 0.2.1

# Check that cuda is available
print( 'cuda is available: ' , torch.cuda.is_available() )

cuda is available:  False

Importing modules from examples_fast

import main

Setting channels for event data...
Channels set.
Setting channels for loaded instrument response (sub)matrix...
Channels set.
No parameters supplied... empty subspace created.
Creating parameter:
    > Named "phase_shift" with fixed value 0.000e+00.
    > The phase shift for the signal, a periodic parameter [cycles].
Creating parameter:
    > Named "frequency" with fixed value 3.140e+02.
    > Spin frequency [Hz].
Creating parameter:
    > Named "mass" with bounds [1.000e+00, 1.600e+00].
    > Gravitational mass [solar masses].
Creating parameter:
    > Named "radius" with bounds [1.000e+01, 1.300e+01].
    > Coordinate equatorial radius [km].
Creating parameter:
    > Named "distance" with bounds [5.000e-01, 2.000e+00].
    > Earth distance [kpc].
Creating parameter:
    > Named "cos_inclination" with bounds [0.000e+00, 1.000e+00].
    > Cosine of Earth inclination to rotation axis.
Creating parameter:
    > Named "super_colatitude" with bounds [1.000e-03, 1.570e+00].
    > The colatitude of the centre of the superseding region [radians].
Creating parameter:
    > Named "super_radius" with bounds [1.000e-03, 1.570e+00].
    > The angular radius of the (circular) superseding region [radians].
Creating parameter:
    > Named "phase_shift" with bounds [-2.500e-01, 7.500e-01].
    > The phase of the hot region, a periodic parameter [cycles].
Creating parameter:
    > Named "super_temperature" with bounds [6.000e+00, 7.000e+00].
    > log10(superseding region effective temperature [K]).
Creating parameter:
    > Named "mode_frequency" with fixed value 3.140e+02.
    > Coordinate frequency of the mode of radiative asymmetry in the
photosphere that is assumed to generate the pulsed signal [Hz].
No parameters supplied... empty subspace created.
Checking likelihood and prior evaluation before commencing sampling...
Not using ``allclose`` function from NumPy.
Using fallback implementation instead.
Checking closeness of likelihood arrays:
-3.1603740790e+04 | -3.1603740790e+04 .....
Closeness evaluated.
Log-likelihood value checks passed on root process.
Checks passed.

Preparing for SBI

First we follow procedures for synthetic data generation that will be used by SBI to generate training data. The SBI_wrapper module consists of multiple classes and functions, including the usual data synthesis process but with some extended functionalities.

_data = SBI_wrapper.SynthesiseData(main.Instrument.channels,
                                   main.data.phases,
                                   0,
                                   len(main.Instrument.channels) - 1)

Setting channels for event data...
Channels set.

main.CustomSignal.synthesise = SBI_wrapper.synthesise
signal = main.CustomSignal(data = _data,
                           instrument = main.Instrument,
                           background = None,
                           interstellar = None,
                           prefix='instr',
                           cache=True)

Creating parameter:
    > Named "phase_shift" with fixed value 0.000e+00.
    > The phase shift for the signal, a periodic parameter [cycles].
No data... can synthesise data but cannot evaluate a likelihood function.

In the code block above, the background has been set to None. In its current form, it’s recommended to either fix the background or use a parameterized functional background model since the default_background_marginalisation is only utilized during the likelihood computation process that SBI skips.

In principle, one may leave the background free and then allow the neural network to simply learn what the background is for any given dataset. However, performance in such a scenario has not been tested, and one may expect that to introduce too much degeneracy in the parameter space for SBI to work meaningfully.

In the code block below, we are using a Custom_SBI_Likelihood that inherits fromt the xpsi.Likelihood class and modifies that _driver and synthesise methods to return model_flux that is the synthesised signal, which then constitutes the training dataset.

likelihood = SBI_wrapper.Custom_SBI_Likelihood(star = main.star,
                                               signals = signal,
                                               prior = main.prior,
                                               num_energies = 64,
                                               threads = 1)
print(likelihood)

Free parameters
---------------
mass: Gravitational mass [solar masses].
radius: Coordinate equatorial radius [km].
distance: Earth distance [kpc].
cos_inclination: Cosine of Earth inclination to rotation axis.
p__phase_shift: The phase of the hot region, a periodic parameter [cycles].
p__super_colatitude: The colatitude of the centre of the superseding region [radians].
p__super_radius: The angular radius of the (circular) superseding region [radians].
p__super_temperature: log10(superseding region effective temperature [K]).

During training, SBI learns the joint data and model space \(P(\theta; D)\), where the model is defined by the free parameters (the ones shown above in this example). In this process, it essentially also approximates the likelihood \(P(D|\theta)\) without explicitly calculating it.

Training SBI

With our prerequisites in place, we first instantiate our simulator and prior for SBI. To do so, we need to inform the sbi package about our pulse profile generator (defined by SBI_wrapper.xpsi_wrappers.simulator) and prior distributions (defined by SBI_wrapper.xpsi_wrappers.sample and SBI_wrapper.xpsi_wrappers.log_prob) for our free model parameters. These methods are in compliance with the requirements of the sbi package for training.

The SBI_wrapper.xpsi_wrappers.simulator calls the synthesise method that we bound to main.CustomSignal above, which in turn requires information about the exposure_time (or expected_source_counts), nchannels and nphases.

The prepare_for_sbi functionality of sbi then checks whether its internal requirements are met, reshapes and typecasts them into usable products for training.

instr_kwargs = dict(exposure_time = 1.0E+06,    # alternatively input
                                                # expected_source_counts
                    nchannels = len(main.Instrument.channels),
                    nphases = len(main.data.phases))

wrapped = xpsi_wrappers(prior = main.prior,
                        likelihood = likelihood,
                        instr_kwargs = instr_kwargs,
                        train_using_CNNs = True)

simulator, prior = prepare_for_sbi(wrapped.simulator, wrapped)

Drawing samples from the joint prior...
Samples drawn.
Drawing samples from the joint prior...
Samples drawn.
Drawing samples from the joint prior...
Samples drawn.
Drawing samples from the joint prior...
Samples drawn.
Drawing samples from the joint prior...

/tmp/ipykernel_36371/4002819185.py:11: DeprecationWarning: This method is deprecated as of sbi version v0.23.0. and will be removed in a         future release.Please use `process_prior` and `process_simulator` in the future.
  simulator, prior = prepare_for_sbi(wrapped.simulator, wrapped)
/home/saltuomo/.conda/envs/xpsi_py3/lib/python3.12/site-packages/sbi/utils/user_input_checks_utils.py:28: UserWarning: No prior bounds were passed, consider passing lower_bound and / or upper_bound if your prior has bounded support.
  self.custom_support = build_support(lower_bound, upper_bound)
/home/saltuomo/.conda/envs/xpsi_py3/lib/python3.12/site-packages/sbi/utils/user_input_checks_utils.py:30: UserWarning: Prior is lacking mean attribute, estimating prior mean from samples.
  self._set_mean_and_variance()

Samples drawn.
Drawing samples from the joint prior...
Samples drawn.
Drawing samples from the joint prior...
Samples drawn.
Drawing samples from the joint prior...
Samples drawn.
Drawing samples from the joint prior...
Samples drawn.
Drawing samples from the joint prior...
Samples drawn.

/home/saltuomo/.conda/envs/xpsi_py3/lib/python3.12/site-packages/sbi/utils/user_input_checks_utils.py:30: UserWarning: Prior is lacking variance attribute, estimating prior variance from samples.
  self._set_mean_and_variance()

Now, we generate training samples. Here we are using 1000 samples for training. This is insufficient for the complexity of the given model and is only used for tutorial purposes. (Tip: Save the training samples for future use. Not done here.)

theta, x = simulate_for_sbi(simulator,
                            proposal=prior,
                            num_simulations=100, #1000,    # Reduced for quick testing
                            num_workers=1)

Drawing samples from the joint prior...
Samples drawn.

Phase-energy-resolved pulse profiles are equivalent to 2D (grayscale) images. Therefore, Convolutional Neural Networks (CNNs) can be utilized, in principle, to better capture neighbouring information between adjacent sets of pixels. xpsi.utilities.Example_CNNs provides a set of CNN architectures, including pre-trained architectures from PyTorch ResNet and ResNeXt.

Below we use the relatively simple CNN architecture C2P1_FC1 to pass onto sbi as an embedding_net for feature retrieval during training. One may also choose to not use any embedding_net and simply pass a flattened 1D pulse profile (or a 1D bolometric pulse profile).

embedding_net = CNNs.C2P1_FC1(nchannels = len(main.Instrument.channels),
                              nphases = len(main.data.phases) - 1)

We now instantiate the neural posterior estimator SNPE, using our sbi-compatible prior and a density_estimator where we specify NN-architecture for this. In this notebook, we have used a Masked Autoregressive Flow (MAF) model architecture. The sbi package documentation details other model architectures that we can use in this regard.

neural_posterior = posterior_nn(model="maf",    # Masked Autoregressive Flow
                                embedding_net=embedding_net,  # skip if not using CNN
                                hidden_features=10,
                                num_transforms=2)
device = "cuda" if torch.cuda.is_available() else "cpu"    # cuda for training on Nvidia GPUs
inference = SNPE(prior=prior, density_estimator=neural_posterior, device=device)

Drawing samples from the joint prior...
Samples drawn.

Time to train! 🏃‍♂️💪

density_estimator = inference.append_simulations(theta, x).train()

 Neural network successfully converged after 754 epochs.

Hooray! 🎉

Note that the number of epochs required for training can vary quite a lot upon re-running this notebook since we are using too few training samples.

Plotting posteriors

posterior = inference.build_posterior(density_estimator)

Drawing samples from the joint prior...
Samples drawn.
Drawing samples from the joint prior...
Samples drawn.

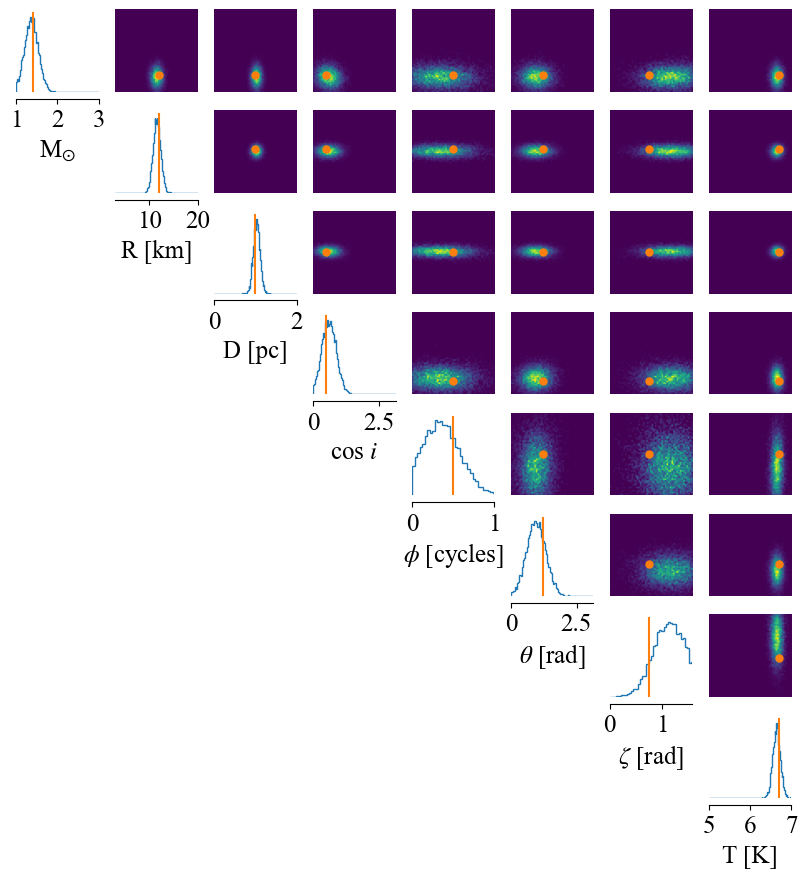
Finally, we plot the posteriors corresponding to an input test observation. We draw 10k samples from the posterior to plot the distribution, using the native plotter in the sbi package.

p = [1.4,  # mass
     12,   # radius
     1.0,  # distance
     math.cos(np.radians(60)),  # inclination
     0.5,  # phase shift
     np.radians(70),  # super colatitude
     0.75, # super radius
     6.7]  # super temperature
test_observation = torch.Tensor(likelihood.synthesise(p, force=True, instr=instr_kwargs))
if torch.cuda.is_available():
    test_observation = test_observation.cuda()

samples = posterior.sample((10000,), x=test_observation)

_ = analysis.pairplot(samples.cpu(),
                      limits=[[1, 3.0], [3, 20], [0.0, 2.0], [0.0, math.pi], [0.0, 1.0], [0.0, math.pi], [0.0, math.pi/2.0], [5.0, 7.0]],
                      figsize=(10, 10),
                      points=np.array(p),
                      labels=[r'M$_{\odot}$', r'R [km]', r'D [pc]', r'cos $i$', r'$\phi$ [cycles]', r'$\theta$ [rad]', r'$\zeta$ [rad]', r'T [K]'])