X-PSI 101 - For Beginners
This tutorial provides a very basic overview of how you can use X-PSI. It models a single hot spot on a neutron star surface and perfoms sampling for parameter estimation. This is a very simplistic model, but gives a very general example for how one can use X-PSI. It allows you to browse all of the different classes available in X-PSI, free of most of the technical details found in the other notebooks. The same steps are followed in the Modeling tutorial, with additional information and a more complex model.
To run this tutorial, all data files should be available in in the directory examples/examples_modeling_tutorial/model_data/.
[1]:
%matplotlib inline
import os
import numpy as np
import math
import time
from matplotlib import pyplot as plt
from matplotlib import rcParams
from matplotlib.ticker import MultipleLocator, AutoLocator, AutoMinorLocator
from matplotlib import gridspec
from matplotlib import cm
rcParams['text.usetex'] = False
rcParams['font.size'] = 14.0
import xpsi
from xpsi.global_imports import _c, _G, _dpr, gravradius, _csq, _km, _2pi
from xpsi.utilities import PlottingLibrary as XpsiPlot
/=============================================\
| X-PSI: X-ray Pulse Simulation and Inference |
|---------------------------------------------|
| Version: 3.0.6 |
|---------------------------------------------|
| https://xpsi-group.github.io/xpsi |
\=============================================/
Check your emcee installation.
Check your installation of emcee if using the EnsembleSampler
Imported PyMultiNest.
Imported UltraNest.
Warning: Cannot import torch and test SBI_wrapper.
Imported GetDist version: 1.5.3
Imported nestcheck version: 0.2.1
Step #1: Data and Instrument Response Files
Data
Let us load the dataset we wish to model. Here a synthetic data set that we generated in advance is called with the Data class, and we know the fictitious exposure time:
[2]:
data = xpsi.Data(counts = np.loadtxt('../../examples/examples_modeling_tutorial/model_data/synthetic_ST_realisation.dat', dtype=np.double),
channels=np.arange(20,201),
phases=np.linspace(0.0, 1.0, 33),
first=0, last=180,
exposure_time=226029523.452384)
Setting channels for event data...
Channels set.
For real data, the X-ray telescope processing pipeline usually results in an event file (EVT) or spectrum (PHA or PI) in FITS format. X-PSI can use both as input (as well as text files), but there is no timing (pulse phase) information in a spectrum file. These files can be loaded with xpsi.Data.load(file_path,n_phases=32, channels=None, phase_column='PULSE_PHASE', channel_column='PI') where :
file_pathpoints to an EVT or PHA or PI filen_phaseis the number of phase bins to divide the data into (for EVT files)channelsgives the list of channels to extractphase_columnis the column to take the phase values from (for EVT files)channel_columnis the column to take the channel values from (for EVT files)
Let’s take a look at the data that we aim to model. We can plot it with a built-in function :
[3]:
fig, axs = data.plot( dpi=100 , colormap='inferno' , num_rot=2)
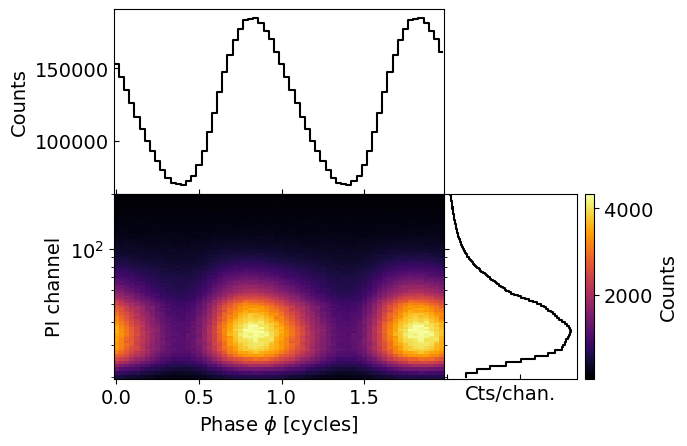
The central plot shows the phase-energy (or phase-channel) pulse profile, caused by the emission from a hot spot on the surface of the neutron star. The right panel is the spectrum (integrated over phases), while the top panel is the bolometric pulse-profile (integrated over channels).
Instrument
We then load an instrument object with the response files of our favourite telescope (NICER in this example), by calling the Instrument class. This lets us transform incident fluxes into expected counts/channel.
[4]:
NICER = xpsi.Instrument.from_ogip_fits(RMF_path='nicer_20170601v003.rmf',
ARF_path='nicer_20170601v005.arf',
datafolder='../../examples/examples_modeling_tutorial/model_data/')
# here we manually trim the instrument response files to restrict to channels 20:200
NICER.trim_response(min_channel=20, max_channel=200, threshold=2.)
Loading instrument response matrix from OGIP compliant files...
Triming the response matrix because it contains columns with only 0 values.
Now min_channel=9 and max_channel=1500
Setting channels for loaded instrument response (sub)matrix...
Channels set.
An empty subspace was created. This is normal behavior - no parameters were supplied.
Response matrix loaded.
Trimming instrument response...
Setting channels for loaded instrument response (sub)matrix...
Channels set.
Triming the response matrix because it contains rows with only values <= 2.0.
Now min_energy=0.17499999701976776 and max_energy=2.2260000705718994
Instrument response trimmed.
A lot of instrument-related information and plotting options can be found in the notebook Instrument synergy.
Signal
We create a Signal class object to store the properties of the instrument and dataset. It is currently the only basic class which also requires definition of a Custom class to implement the background marginalisation method. Here we choose to use the default class, but other methods have been implemented, available in the likelihoods/ directory. It can also store background information (either through a Background model or a support file, loaded the same way as Data) and
interstellar attenuation (using the Interstellar class, which also requires a Custom class to compute the attenuation).
[5]:
from xpsi.likelihoods.default_background_marginalisation import eval_marginal_likelihood
from xpsi.likelihoods.default_background_marginalisation import precomputation
class CustomSignal(xpsi.Signal):
"""
A custom calculation of the logarithm of the likelihood.
We extend the :class:`~xpsi.Signal.Signal` class to make it callable.
We overwrite the body of the __call__ method. The docstring for the
abstract method is copied.
"""
def __init__(self, workspace_intervals = 1000, epsabs = 0, epsrel = 1.0e-8,
epsilon = 1.0e-3, sigmas = 10.0, support = None, **kwargs):
""" Perform precomputation.
:params ndarray[m,2] support:
Prior support bounds for background count rate variables in the
:math:`m` instrument channels, where the lower bounds must be zero
or positive, and the upper bounds must be positive and greater than
the lower bound. Alternatively, setting the an upper bounds as
negative means the prior support is unbounded and the flat prior
density functions per channel are improper. If ``None``, the lower-
bound of the support for each channel is zero but the prior is
unbounded.
"""
super(CustomSignal, self).__init__(**kwargs)
try:
self._precomp = precomputation(self._data.counts.astype(np.int32))
except AttributeError:
print('Warning: No data... can synthesise data but cannot evaluate a '
'likelihood function.')
else:
self._workspace_intervals = workspace_intervals
self._epsabs = epsabs
self._epsrel = epsrel
self._epsilon = epsilon
self._sigmas = sigmas
if support is not None:
self._support = support
else:
self._support = -1.0 * np.ones((self._data.counts.shape[0],2))
self._support[:,0] = 0.0
def __call__(self, *args, **kwargs):
self.loglikelihood, self.expected_counts, self.background_signal, self.background_given_support = \
eval_marginal_likelihood(self._data.exposure_time,
self._data.phases,
self._data.counts,
self._signals,
self._phases,
self._shifts,
self._precomp,
self._support,
self._workspace_intervals,
self._epsabs,
self._epsrel,
self._epsilon,
self._sigmas,
kwargs.get('llzero'),
allow_negative=(False))
[6]:
signal = CustomSignal(data = data,
instrument = NICER,
background = None,
interstellar = None,
workspace_intervals = 1000,
cache = True,
epsrel = 1.0e-8,
epsilon = 1.0e-3,
sigmas = 10.0,
support = None)
Creating parameter:
> Named "phase_shift" with fixed value 0.000e+00.
> The phase shift for the signal, a periodic parameter [cycles].
Step #2: Create an emission model
Constructing a star
We now need to build our star model. The building blocks of our very simple star are:
the Spacetime class, a model of the ambient Schwarzschild spacetime;
the HotRegion class, a model for a hot spot on the surface of the neutron star;
the Photosphere class, a model of the rotating neutron star photosphere.
In this example, we assume that only one hot spot is responsible for the emission of the Photosphere in the X-ray band for our instrument. Hence, we use just a simple HotRegion model.
To instantiate each of those basic units, we need to define the relevant parameters (including mass, radius, hot spot size, etc). Each of the parameters must be defined in one of two ways :
either by providing bounds, in which case the parameter is free to move between the given bounds;
or as a value, in which case the parameter is fixed at said value.
If both bounds and a value are provided for one parameter, this parameter will have the given value as an initial value but will be set free to vary between the bounds. The required and optional parameter names can be found in the class API.
The ambient spacetime
[7]:
## First example : we provide ONLY values for all of the parameters, and no bounds. In this case, all the parameters are fixed.
values = dict(distance = 0.150, # (Earth) distance
mass = 1.5, # mass
radius = 12.0, # equatorial radius
cos_inclination = 0.5, # (Earth) inclination to rotation axis
frequency = 300. ) # spin frequency
spacetime = xpsi.Spacetime(bounds={}, values=values)
Creating parameter:
> Named "frequency" with fixed value 3.000e+02.
> Spin frequency [Hz].
Creating parameter:
> Named "mass" with fixed value 1.500e+00.
> Gravitational mass [solar masses].
Creating parameter:
> Named "radius" with fixed value 1.200e+01.
> Coordinate equatorial radius [km].
Creating parameter:
> Named "distance" with fixed value 1.500e-01.
> Earth distance [kpc].
Creating parameter:
> Named "cos_inclination" with fixed value 5.000e-01.
> Cosine of Earth inclination to rotation axis.
[8]:
## Another example is to give only bounds for some, only values for others, or both (for the mass here)
bounds = dict(distance = (None, None), # Default bounds for (Earth) distance
mass = (None, None), # Default bounds for mass
radius = (None, None), # Default bounds for equatorial radius
cos_inclination = (None, None)) # Default bounds for (Earth) inclination to rotation axis
values = dict(frequency=300.0, # Fixed spin frequency
mass=1.4) # mass with initial value
spacetime = xpsi.Spacetime(bounds=bounds, values=values)
Creating parameter:
> Named "frequency" with fixed value 3.000e+02.
> Spin frequency [Hz].
Creating parameter:
> Named "mass" with bounds [1.000e-03, 3.000e+00] and initial value 1.400e+00.
> Gravitational mass [solar masses].
Creating parameter:
> Named "radius" with bounds [1.000e+00, 2.000e+01].
> Coordinate equatorial radius [km].
Creating parameter:
> Named "distance" with bounds [1.000e-02, 3.000e+01].
> Earth distance [kpc].
Creating parameter:
> Named "cos_inclination" with bounds [-1.000e+00, 1.000e+00].
> Cosine of Earth inclination to rotation axis.
For the following example in this tutorial, we will specify bounds for all parameters except for the frequency, which will be fixed.
[9]:
bounds = dict(distance = (1.0,10.0), # distance in kpc
mass = (1.0, 3.0), # mass with default bounds
radius = (3.0 * gravradius(1.0), 16.0), # equatorial radius
cos_inclination = (0.0, 1.0)) # (Earth) inclination to rotation axis
values = dict(frequency=200.0) # Fixed spin frequency
spacetime = xpsi.Spacetime(bounds=bounds, values=values)
Creating parameter:
> Named "frequency" with fixed value 2.000e+02.
> Spin frequency [Hz].
Creating parameter:
> Named "mass" with bounds [1.000e+00, 3.000e+00].
> Gravitational mass [solar masses].
Creating parameter:
> Named "radius" with bounds [4.430e+00, 1.600e+01].
> Coordinate equatorial radius [km].
Creating parameter:
> Named "distance" with bounds [1.000e+00, 1.000e+01].
> Earth distance [kpc].
Creating parameter:
> Named "cos_inclination" with bounds [0.000e+00, 1.000e+00].
> Cosine of Earth inclination to rotation axis.
In order to create a Photosphere object, which will describe the surface emission, we first have to build up the emitting region(s), through a HotRegion object.
For simplicity, we instantiate a single HotRegion object with a simple circular hot spot described by one single temperature (the ‘ST’ model) at the surface. For details of the names and descriptions of more complex regions, check the notebook Hot region complexity. For this example, the default blackbody atmosphere model is used.
[10]:
bounds = dict(super_colatitude = (None, None), # latitude of the hot spot in radians, from north pole (default: 0) to south pole (default: pi)
super_radius = (None, None), # radius of the hot spot, in radians (default: between 0 and pi/2 (half of the NS))
phase_shift = (-0.25, 0.75), # longitude of the hot spot
super_temperature = (None, None)) # temperature of the hot spot, default: 3.0 to 7.6, from very cold to very hot
# a simple circular, simply-connected spot
primary = xpsi.HotRegion(bounds=bounds,
values={}, # no initial values and no derived/fixed values
symmetry=True,
omit=False,
cede=False,
concentric=False,
sqrt_num_cells=32,
min_sqrt_num_cells=10,
max_sqrt_num_cells=64,
num_leaves=64,
num_rays=200,
atm_ext="BB", # default blackbody, other options: "Num4D" or "user"
prefix='p') # unique prefix to identify the region, needed if >1 instances
Creating parameter:
> Named "super_colatitude" with bounds [0.000e+00, 3.142e+00].
> The colatitude of the centre of the superseding region [radians].
Creating parameter:
> Named "super_radius" with bounds [0.000e+00, 1.571e+00].
> The angular radius of the (circular) superseding region [radians].
Creating parameter:
> Named "phase_shift" with bounds [-2.500e-01, 7.500e-01].
> The phase of the hot region, a periodic parameter [cycles].
Creating parameter:
> Named "super_temperature" with bounds [3.000e+00, 7.600e+00].
> log10(superseding region effective temperature [K]).
We now need to encapsulate the HotRegion instance in a Photosphere class.
[11]:
photosphere = xpsi.Photosphere(hot = primary, elsewhere = None,
values=dict(mode_frequency = spacetime['frequency']))
Creating parameter:
> Named "mode_frequency" with fixed value 2.000e+02.
> Coordinate frequency of the mode of radiative asymmetry in the
photosphere that is assumed to generate the pulsed signal [Hz].
Star
We can now combine the ambient spacetime, Spacetime, and the embedded photosphere, Photosphere, into a model star represented by an instance of Star, as follows:
[12]:
star = xpsi.Star(spacetime = spacetime, photospheres = photosphere)
Prior
We can now make a Prior object which will contain all of the information and constraints that we have on our parameters prior to sampling. The default prior only checks that sampled values are within the given bounds for the free parameters. If more information is available, a Custom class can be created, as follows, to store and apply these constraints during sampling. Here we implement a joint constraint on the gravitational mass and equatorial radius to assign zero prior density to
stars which are too compact (for more on compactness limits see Lattimer & Prakash (2001)).
[13]:
from scipy.stats import truncnorm
class CustomPrior(xpsi.Prior):
""" A custom (joint) prior distribution.
Source: Fictitious
Model variant: ST-U
Two single-temperature, simply-connected circular hot regions with
unshared parameters.
"""
__derived_names__ = ['compactness', ]
__draws_from_support__ = 3
def __init__(self):
""" Nothing to be done.
A direct reference to the spacetime object could be put here
for use in __call__:
.. code-block::
self.spacetime = ref
Instead we get a reference to the spacetime object through the
a reference to a likelihood object which encapsulates a
reference to the spacetime object.
"""
super(CustomPrior, self).__init__() # not strictly required if no hyperparameters
def __call__(self, p = None):
""" Evaluate distribution at ``p``.
:param list p: Model parameter values.
:returns: Logarithm of the distribution evaluated at ``p``.
"""
temp = super(CustomPrior, self).__call__(p)
if not np.isfinite(temp):
return temp
# based on contemporary EOS theory
if not self.parameters['radius'] <= 16.0:
return -np.inf
ref = self.parameters.star.spacetime # shortcut
# limit polar radius to try to exclude deflections >= \pi radians
# due to oblateness this does not quite eliminate all configurations
# with deflections >= \pi radians
R_p = 1.0 + ref.epsilon * (-0.788 + 1.030 * ref.zeta)
if R_p < 1.76 / ref.R_r_s:
return -np.inf
# polar radius at photon sphere for ~static star (static ambient spacetime)
#if R_p < 1.5 / ref.R_r_s:
# return -np.inf
mu = math.sqrt(-1.0 / (3.0 * ref.epsilon * (-0.788 + 1.030 * ref.zeta)))
# 2-surface cross-section have a single maximum in |z|
# i.e., an elliptical surface; minor effect on support, if any,
# for high spin frequenies
if mu < 1.0:
return -np.inf
ref = self.parameters # redefine shortcut
return 0.0
def inverse_sample(self, hypercube=None):
""" Draw sample uniformly from the distribution via inverse sampling. """
to_cache = self.parameters.vector
if hypercube is None:
hypercube = np.random.rand(len(self))
# the base method -a uniform sampling within the bounds- is useful, so to avoid writing that code again:
_ = super(CustomPrior, self).inverse_sample(hypercube)
ref = self.parameters # shortcut
# flat priors in cosine of hot region centre colatitudes (isotropy)
# support modified by no-overlap rejection condition
idx = ref.index('p__super_colatitude')
a, b = ref.get_param('p__super_colatitude').bounds
a = math.cos(a); b = math.cos(b)
ref['p__super_colatitude'] = math.acos(b + (a - b) * hypercube[idx])
# restore proper cache
for parameter, cache in zip(ref, to_cache):
parameter.cached = cache
# it is important that we return the desired vector because it is
# automatically written to disk by MultiNest and only by MultiNest
return self.parameters.vector
def transform(self, p, **kwargs):
""" A transformation for post-processing. """
p = list(p) # copy
# used ordered names and values
ref = dict(zip(self.parameters.names, p))
# compactness ratio M/R_eq
p += [gravradius(ref['mass']) / ref['radius']]
return p
[14]:
prior = CustomPrior()
An empty subspace was created. This is normal behavior - no parameters were supplied.
Likelihood
We can now construct and instantiate a Likelihood object. With this we will be able to do likelihood evaluation using the model components defined above.
[15]:
likelihood = xpsi.Likelihood(star = star, signals = signal,
prior = prior,
num_energies=128,
threads=1,
externally_updated=False)
We can retrieve the free model parameters:
[16]:
likelihood
[16]:
Free parameters
---------------
mass: Gravitational mass [solar masses].
radius: Coordinate equatorial radius [km].
distance: Earth distance [kpc].
cos_inclination: Cosine of Earth inclination to rotation axis.
p__phase_shift: The phase of the hot region, a periodic parameter [cycles].
p__super_colatitude: The colatitude of the centre of the superseding region [radians].
p__super_radius: The angular radius of the (circular) superseding region [radians].
p__super_temperature: log10(superseding region effective temperature [K]).
Note that if you want to modify the definition of the model parameter space you should construct a new likelihood object, instead of manipulating existing objects, for safety. (You can also restart the kernel, although if this is required it is a bug.)
We can give this object some parameters and compute a likelihood, or compare it to a known likelihood as a check.
[17]:
p = [1.4, # mass
12.0, # radius
5.2, # distance
0.4, # cos_inclination
0.1, # p__phase_shift
0.9, # p__super_colatitude
0.2, # p__super_radius
6.15] # p__super_temperature
## You can evaluate the likelihood for the parameters p
print(likelihood(p, reinitialise=True)) # use reinitialise=True if settings have been changed since the last call of the likelihood (here it is not necessary)
## Or check that you get the expected likelihood value
likelihood.clear_cache()
t = time.time()
likelihood.check(None, [-27551.546372710967], 1.0e-6,
physical_points=[p])
print('time = %.3f s' % (time.time() - t))
-27551.546372710967
Checking likelihood and prior evaluation before commencing sampling...
Not using ``allclose`` function from NumPy.
Using fallback implementation instead.
Checking closeness of likelihood arrays:
-2.7551546373e+04 | -2.7551546373e+04 .....
Closeness evaluated.
Log-likelihood value checks passed on root process.
Checks passed.
time = 0.163 s
Calling the Likelihood object created (or overwrote) the signal.expected_counts (counts/chan predicted by the current model) which can be compared to signal.data.counts (counts/chan from data file).
Inspecting functionality
Let’s plot our pulse and our hot spot configuration. First, the 1D (bolometric) pulse profile, and the 2D (energy-resolved) pulse profile.
[18]:
XpsiPlot.plot_1d_pulse(signal=signal,
photosphere=photosphere,
photosphere_phases=signal.phases)
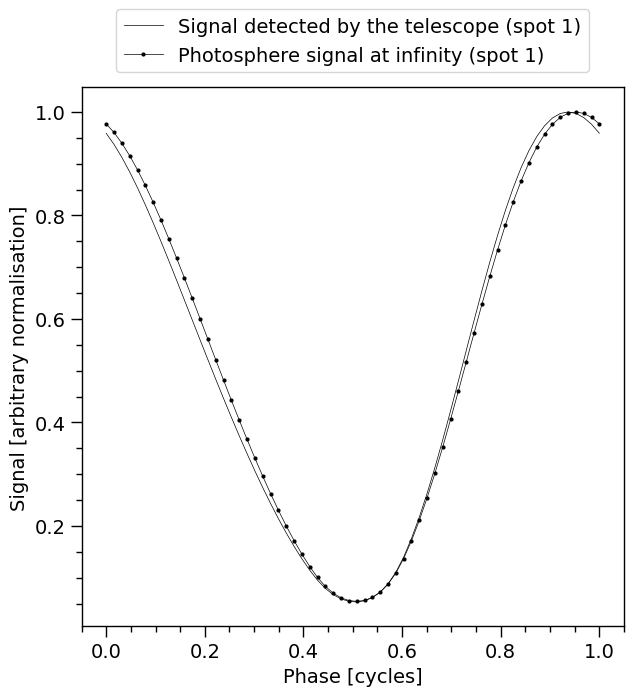
Photosphere (the points with the markers) is the signal that is observed outside the potential well of the star. It is the signal that would be observed at infinity in vacuum. The markers represent the phase resolution. On the other hand, Signal (without markers) is the effective signal that is detected by the telescope (after interstellar absorption and instrument response effects). The latter is compared to the data for the likelihood computation.
[19]:
XpsiPlot.plot_2d_pulse(pulse=signal.data.counts,
x=data.phases,
y=data.channels,
rotations=2,
ylabel='Channel',
cbar_label='Counts',)
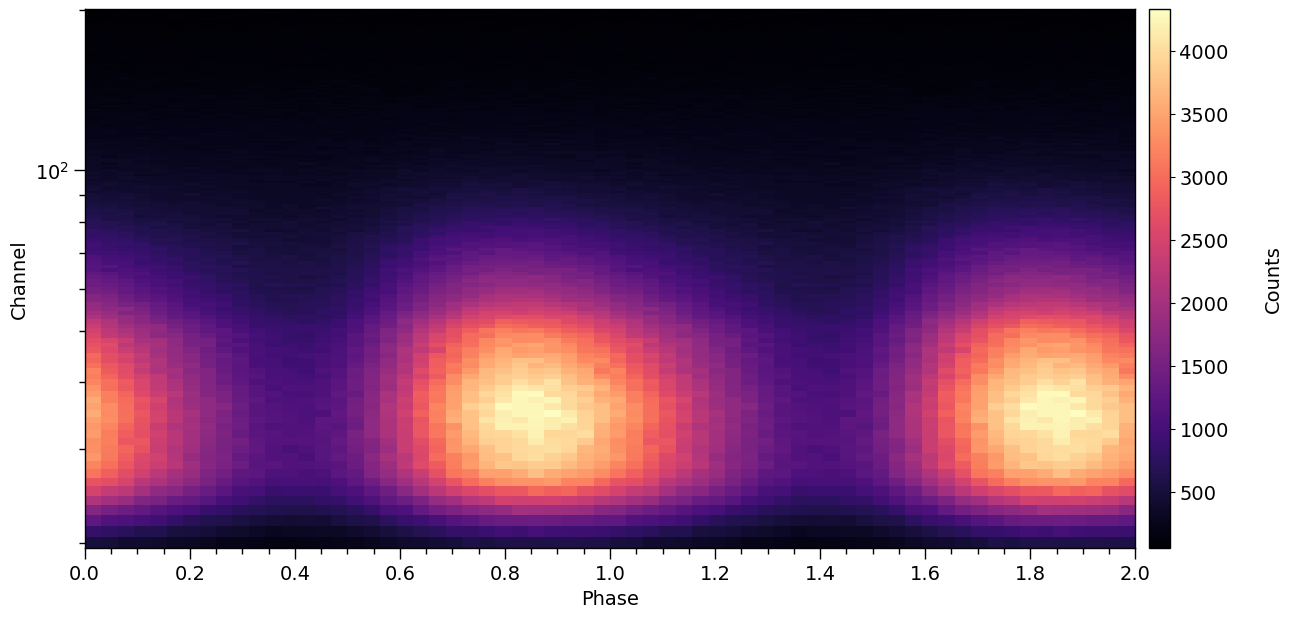
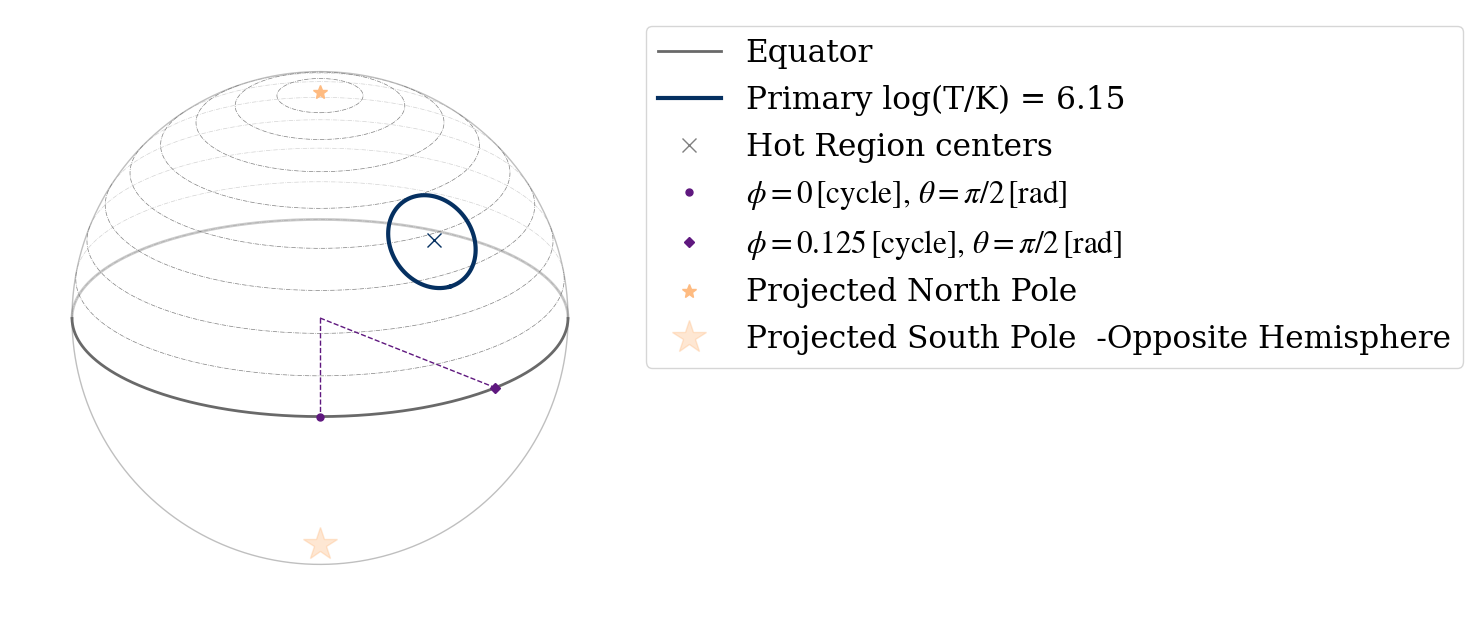
We can also use the projection tool to visualize the geometry of the neutron star hot region (see the Emitting Patterns 2D Projection notebook for more information about the tool):
[20]:
from xpsi.utilities import ProjectionTool
ProjectionTool.plot_projection_general((likelihood),"ST","I","NP")
YOU ARE USING 1 HOT SPOT MODEL
[20]:
<Axes: >
Sampling interface
We have constructed and instantiated a Likelihood object, containing the data and instrument response files, as well as the star model and all of our priors. We are now ready for sampling. Several samplers are availbale in X-PSI for that purpose: PyMultiNest, emcee, or UltraNest. In this example we will use Multinest, but examples with the other
samplers can be found in the Modeling notebook.
MultiNest
We interface with the nested sampler MultiNest by defining some runtime settings, and then passing those settings together with likelihood and prior objects to a wrapper from the Sample module. We will run the sampler for a specified number (100) of nested replacements (iterations).
The environment variable LD_LIBRARY_PATH must be set before launching Jupyter as follows:
$ export LD_LIBRARY_PATH=<path/to/multinest>/lib
Get the parameters that are periodic or wrapped to inform MultiNest of boundary properties:
[21]:
wrapped_params = [0]*len(likelihood)
wrapped_params[likelihood.index('p__phase_shift')] = 1
[ ]:
os.system("mkdir -p Output")
runtime_params = {'resume': True,
'importance_nested_sampling': False,
'multimodal': False,
'n_clustering_params': None,
'outputfiles_basename': './Output/run', # make ./Output directory manually
'n_iter_before_update': 5,
'n_live_points': 100,
'sampling_efficiency': 0.8,
'const_efficiency_mode': False,
'wrapped_params': wrapped_params,
'evidence_tolerance': 0.5,
'max_iter': 500, # manual termination condition for short test
'verbose': True}
likelihood.threads = 1
likelihood.reinitialise()
likelihood.clear_cache()
# inform source code that parameter objects updated when inverse sampling
likelihood.externally_updated = True
xpsi.Sample.nested(likelihood, prior, **runtime_params)
Commencing integration...
Sampling efficiency set to: 1.6456.
*****************************************************
MultiNest v3.12
Copyright Farhan Feroz & Mike Hobson
Release Nov 2019
no. of live points = 100
dimensionality = 8
resuming from previous job
*****************************************************
Starting MultiNest
/tmp/ipykernel_731636/3575453599.py:52: DeprecationWarning: Conversion of an array with ndim > 0 to a scalar is deprecated, and will error in future. Ensure you extract a single element from your array before performing this operation. (Deprecated NumPy 1.25.)
eval_marginal_likelihood(self._data.exposure_time,
Acceptance Rate: 0.455182
Replacements: 650
Total Samples: 1428
Nested Sampling ln(Z): -233283.459920
Acceptance Rate: 0.454841
Replacements: 700
Total Samples: 1539
Nested Sampling ln(Z): -211941.504547
Acceptance Rate: 0.444313
Replacements: 750
Total Samples: 1688
Nested Sampling ln(Z): -187027.194483
Acceptance Rate: 0.445186
Replacements: 800
Total Samples: 1797
Nested Sampling ln(Z): -164001.726236
Acceptance Rate: 0.445960
Replacements: 850
Total Samples: 1906
Nested Sampling ln(Z): -132206.611617
Acceptance Rate: 0.441393
Replacements: 900
Total Samples: 2039
Nested Sampling ln(Z): -111995.235175
Acceptance Rate: 0.434186
Replacements: 950
Total Samples: 2188
Nested Sampling ln(Z): -89870.932719
Acceptance Rate: 0.425713
Replacements: 1000
Total Samples: 2349
Nested Sampling ln(Z): -72819.038724
Acceptance Rate: 0.420842
Replacements: 1050
Total Samples: 2495
Nested Sampling ln(Z): -61421.609338
Acceptance Rate: 0.415565
Replacements: 1100
Total Samples: 2647
Nested Sampling ln(Z): -52322.536639
ln(ev)= -52322.536639264457 +/- NaN
Total Likelihood Evaluations: 2647
Sampling finished. Exiting MultiNest
analysing data from ./Output/run.txt
Integration completed.
See the MultiNest documentation for details on the parameters, and for typical parameter values used in X-PSI, see the Publications.
Once the sampling is finished, the output files (created in the Output/ folder here) can be given to the Post-Processing notebook to visualize and plot the posterior distributions of the parameters.
A typical corner plot that can be produced in Post-Processing following a converged sampling is represented below.
Summary
In this notebook we showed in a very simple way how to use X-PSI to do pulse profile modeling and parameter inference. We constructed a model of a single hot spot on the neutron star surface, including an instrument response, and combined it with data to form a likelihood object. We then defined priors, which together allowed for posterior sampling and parameter inference.