Piecewise Polytropic with ADM Example
To run this tutorial, you should install NEoST following the install guide.
Before continuing with this tutorial, please read the inference process overview to familiarise yourself with the way NEoST parametrises the equation of state.
The following block of code will properly import NEoST and its prerequisites, furthermore it also defines a name for the inference run, this name is what will be prefixed to all of NEoST’s output files.
[1]:
import neost
import kalepy
from neost.eos import polytropes
from neost.Prior import Prior
from neost.Star import Star
from neost.Likelihood import Likelihood
from neost import PosteriorAnalysis
from scipy.stats import multivariate_normal
from scipy.stats import gaussian_kde
import numpy as np
import matplotlib
from matplotlib import pyplot as plt
from pymultinest.solve import solve
import time
import os
import neost.global_imports as global_imports
# Some physical constants
c = global_imports._c
G = global_imports._G
Msun = global_imports._M_s
pi = global_imports._pi
rho_ns = global_imports._rhons
Equation of state object
With NEoST properly imported the equation of state needs to be defined. For the PP parametrisation this is done by creating a polytropes.PolytropicEoS() object. This object takes as input the crust parameter, the rho_t parameter, adm_type string parameter, dm_halo boolean parameter, and two_fluid_tidal boolean parameter.
Valid input for the crust parameter consists of one of the following values: 'ceft-Hebeler', 'ceft-Tews', 'ceft-Lynn', 'ceft-Drischler', 'ceft-old', 'ceft-Keller-N2LO', 'ceft-Keller-N3LO' or None. This instructs NEoST on which cEFT model to use, in order of listing these would be: the band based on the work by Hebeler et al., Tews et al., Lynn et al., Drischler et al., Keller et al. (2024), an old implementation of the Hebeler band from Raaijmakers et al., or no
cEFT at all.
The rho_t parameter tells NEoST at which density to transition between the cEFT crust parametrisation and the core parametrisation. This value must not exceed a value of twice the nuclear saturation density, although for the currently implemented cEFT models it should not exceed 1.1 (1.5 for the Keller bands) times the nuclear saturation density.
The adm_type string parameter tells NEoST which ADM particle type to use from teh Ann Nelson et al. (2018) paper, namely a spin-0 boson or a spin-1/2 dirac fermion. This parameter is defaulted to None, so that it does not need to be defined in an analysis with only baryonic matter.
The dm_halo boolean parameter tells NEoST to calculate ADM halos (or not) when solving the two-fluid TOV equations in TOVdm.pyx or TOVdm_python.py. This parameter is defaulted to False, but we wanted to demonstrate where this value is set by the user. Thus, the inclusion of this parameter is only necessary if the user wishes to include ADM halos or not.
The two_fluid_tidal boolean parameter tells NEoST to calculate the two-fluid tidalformability when solving the two-fluid TOV equations in TOVdm.pyx or TOVdm_python.py. This parameter is defaulted to False, but we wanted to demonstrate where this value is set by the user. Thus, the inclusion of this parameter is only necessary if the user wishes to calculate the tidal deformability of an ADM admixed neutron star.
[2]:
# Define name for run, extra - at the end is for nicer formatting of output
run_name = "PP-example-bosonic-adm-run"
directory = '../../examples/chains'
# We're exploring a polytropic (PP) EoS parametrization with a chiral effective field theory (cEFT) parametrization based on Hebeler's work
# Transition between PP parametrisation and cEFT parametrization occurs at 1.1*saturation density
polytropes_pp = polytropes.PolytropicEoS(crust = 'ceft-Hebeler', rho_t = 1.1*rho_ns, adm_type = 'Bosonic',dm_halo = False,two_fluid_tidal = False)
This block of code defines the measurements used to create the likelihood function for the Bayesian analysis. It shows you how to define measurements for both SciPy and KalePy, as well as what parameters need to be past for a mass-radius measurement and for a gravitational wave event when using non-synthetic data. Note, this example does not include the gravitational waves event data, see the `PP_example’ script for how to include it.
To define a mass-radius measurement you need to create a KDE object. For both KalePy and SciPy, you need to provide the samples from which to create the KDE. These samples need to be provided as an array of shape (2,n) where n is the number of samples of your dataset. The first row should consist of the masses and the second row should consist of the radii. As shown in the example, to turn a dataset into a SciPy KDE consists of simply calling the gaussian_kde() function and providing
the dataset as argument.
To define a gravitational wave event you again have to create a KDE, again the format of the dataset is the same for both a KalePy and a SciPy KDE, but this time the array needs to have a shape of (4,n) where n again is the number of samples in your dataset. Here the rows correspond to the following quantities respectively:
The chirp mass \(M_c\)
The mass ratio \(Q\)
The tidal deformability of the primary \(\Lambda_1\)
The tidal deformability of the secondary \(\Lambda_2\)
For the purposes of this example script we now turn this dataset into a KalePy KDE. We do this by creating a kalepy.KDE() object which takes as first argument your dataset, as second argument you provide the reflection bounds of your KDE for each row in your dataset, where None indicates no reflection. The weights argument provides the weights of your dataset, if your dataset is equally-weighted you do not need to provide this argument. The bandwidth parameter allows you to tweak
the width of the kernels in your KDE and the kernel argument allows you to specify which kernel you want to use.
Next, these KDEs need to be passed to NEoST, this is done through the likelihood_functions and likelihood_params lists. The first one is a list of all the (callable) KDEs, and the second one is a list of as many instances of ['Mass', 'Radius'] as you have mass-radius measurements. The ordering of this list matters insofar as that you need to put any mass-radius measurements first in the likelihood_functions list and any gravitational wave events second.
You will also need to define a chirp_mass list containing the median values of the chirp masses of your events, in case your event is a mass-radius measurement, enter None instead.
Finally you will also need to define how many events you pass to NEoST, a quick and easy way to do this is shown in the example code below.
This block also sets the variable_params depending on the adm_type value since the physical prior spaces of bosonic and fermionic ADM differ by virtue of their differing physical natures. Regardless of the adm_type, bot have three parameters: mchi the ADM particle mass in units of MeV, gchi_over_mphi the effective ADM self-repulsion strength in units of 1/MeV, and adm_fraction is the ADM mass-fraction defined at M_chi/M_total*100, where M_chi is the total accumulated ADM
gravitational mass and M_total is the sum of M_chi and the total baryonic gravitational mass.
With our data defined, the next step is to define both the prior and the likelihood function.
The prior is defined through a pair of dictionaries, variable_params and static_params. Here variable_params takes in the equation of state parameters that will be allowed to vary, and static_params will take in those that won’t. Entries into variable_params should be formatted as follows: 'param_name':[lower_bound,upper_bound]
Additionally, for each of the measurements you must also append a dictionary item 'rhoc_i':[14.6, 16] to the end of variable_params, this parameter covers the central density of star i and needs to be appended for each star individually. Entries into static_params should be formatted in the following manner: 'param_name':value.
[3]:
# Create the likelihoods for the individual measurements
# First we load the mass-radius measurement
mass_radius_j0740 = np.load('../../examples/j0740.npy').T
J0740_LL = gaussian_kde(mass_radius_j0740)
# Pass the likelihoods to the solver
likelihood_functions = [J0740_LL]
likelihood_params = [['Mass', 'Radius']]
# Define whether event is GW or not and define number of stars/events
chirp_mass = [None]
number_stars = len(chirp_mass)
# Define variable parameters, same prior as previous papers of Raaijmakers et al.
if polytropes_pp.adm_type == 'Bosonic':
variable_params={'ceft':[polytropes_pp.min_norm, polytropes_pp.max_norm],'gamma1':[1.,4.5],'gamma2':[0.,8.],'gamma3':[0.5,8.],'rho_t1':[1.5,8.3],'rho_t2':[1.5,8.3],
'mchi':[-2, 8],'gchi_over_mphi': [-3,3],'adm_fraction':[0., 5.]}
elif polytropes_pp.adm_type == 'Fermionic':
variable_params={'ceft':[polytropes_pp.min_norm, polytropes_pp.max_norm],'gamma1':[1.,4.5],'gamma2':[0.,8.],'gamma3':[0.5,8.],'rho_t1':[1.5,8.3],'rho_t2':[1.5,8.3],
'mchi':[-2, 9],'gchi_over_mphi': [-5,3],'adm_fraction':[0., 5.]}
else:
variable_params={'ceft':[polytropes_pp.min_norm, polytropes_pp.max_norm],'gamma1':[1.,4.5],'gamma2':[0.,8.],'gamma3':[0.5,8.],'rho_t1':[1.5,8.3],'rho_t2':[1.5,8.3]}
#Note if the user wants to have a seperate adm_fraction per source, include it below via
#'adm_fraction_' + str(i+1):[0., 5.]. And eliminate the adm_fraction above, as that is to assume all Neutron stars have the same amount of adm_fraction
for i in range(number_stars):
variable_params.update({'rhoc_' + str(i+1):[14.6, 16]})
# Define static parameters, empty dict because all params are variable
static_params={}
If instead you are using synthetic data, for example a 2-dimensional Gaussian distribution, you can define a function that calculates the likelihood directly and pass this on to NEoST as follows:
# 2-dimensional approximation of the J0740 measurement
mu_M = 2.08
mu_R = 11.155
sigma_M = 0.07
sigma_R = 0.1 # uncertainty in radius
J0740 = sps.multivariate_normal(mean=[muM, muR], cov=[[sigM, 0.0], [0.0, sigR]])
likelihood_functions = [J0740.pdf]
likelihood_params = [['Mass', 'Radius']]
Finally, the prior object must be created using the following function call:neost.Prior.Prior(EOS, variable_params, static_params, chirp_masses) where the EOS argument is the equation of state object that was created in the previous step. When this prior is called it will then uniformly sample sets of parameters from the defined parameter ranges.
The likelihood is defined by providing both the previously defined prior object and the likelihood functions defined in the previous codeblock. This is done with the following code: likelihood = Likelihood(prior, likelihood_functions, likelihood_params, chirp_mass)
After defining your prior and likelihood function, it is best practice to test your prior and likelihood function. This is done with the short loop in the code block below. This loop will for each iteration first take a sample from the prior, and then compute the corresponding likelihood of said prior sample and print the likelihood as output.
[4]:
# Define joint prior and joint likelihood
prior = Prior(polytropes_pp, variable_params, static_params, chirp_mass)
likelihood = Likelihood(prior, likelihood_functions, likelihood_params, chirp_mass)
print("Bounds of prior are")
print(variable_params)
print("number of parameters is %d" %len(variable_params))
# Perform a test, this will draw 50 random points from the prior and calculate their likelihood
print("Testing prior and likelihood")
cube = np.random.rand(50, len(variable_params))
for i in range(len(cube)):
par = prior.inverse_sample(cube[i])
print(likelihood.call(par))
print("Testing done")
Bounds of prior are
{'ceft': [1.676, 2.814], 'gamma1': [1.0, 4.5], 'gamma2': [0.0, 8.0], 'gamma3': [0.5, 8.0], 'rho_t1': [1.5, 8.3], 'rho_t2': [1.5, 8.3], 'mchi': [-2, 8], 'gchi_over_mphi': [-3, 3], 'adm_fraction': [0.0, 5.0], 'rhoc_1': [14.6, 16]}
number of parameters is 10
Testing prior and likelihood
-1e+101
-1e+101
-1e+101
-1e+101
-1e+101
-1e+101
-1e+101
-1e+101
-1e+101
-1e+101
-1e+101
-1e+101
-1e+101
-1e+101
-682.6167116235399
-1e+101
-1e+101
-1e+101
-1e+101
-1e+101
-1e+101
-1e+101
-1e+101
-515.7785534718939
-1e+101
-1e+101
-1e+101
-1e+101
-1e+101
-55.01048782217265
-2.5859247697962586
-1e+101
-1e+101
-1e+101
-1e+101
-1e+101
-1e+101
-1e+101
-1e+101
-1e+101
-1e+101
-1e+101
-1e+101
-1e+101
-1e+101
-1e+101
-1e+101
-117.72559467516872
-1e+101
-1e+101
Testing done
When finished with testing your likelihood and prior you can proceed to the actual inference process. This is done in the code block below. Warning: depending on the performance of your platform, this might be a very slow process. To make it slightly faster, we have decreased the number of live points and set a maximum number of iterations for this example. For a proper analysis, we would remove the max_iter argument and set, for example, n_live_points=2000.
[5]:
# Then we start the sampling with MultiNest
start = time.time()
result = solve(LogLikelihood=likelihood.call, Prior=prior.inverse_sample, n_live_points=500, evidence_tolerance=0.1,
n_dims=len(variable_params), sampling_efficiency=0.8, outputfiles_basename=f'{directory}/{run_name}', verbose=True, resume=False)
end = time.time()
print(end - start)
*****************************************************
MultiNest v3.10
Copyright Farhan Feroz & Mike Hobson
Release Jul 2015
no. of live points = 500
dimensionality = 10
*****************************************************
Starting MultiNest
generating live points
live points generated, starting sampling
Acceptance Rate: 0.998185
Replacements: 550
Total Samples: 551
Nested Sampling ln(Z): -541.923303
Importance Nested Sampling ln(Z): -1.541710 +/- 0.094288
Acceptance Rate: 0.988468
Replacements: 600
Total Samples: 607
Nested Sampling ln(Z): -384.333165
Importance Nested Sampling ln(Z): -1.507901 +/- 0.089432
Acceptance Rate: 0.974513
Replacements: 650
Total Samples: 667
Nested Sampling ln(Z): -274.315762
Importance Nested Sampling ln(Z): -1.514281 +/- 0.084774
Acceptance Rate: 0.949796
Replacements: 700
Total Samples: 737
Nested Sampling ln(Z): -155.951502
Importance Nested Sampling ln(Z): -1.535241 +/- 0.081415
Acceptance Rate: 0.912409
Replacements: 750
Total Samples: 822
Nested Sampling ln(Z): -85.244435
Importance Nested Sampling ln(Z): -1.506086 +/- 0.076132
Acceptance Rate: 0.883978
Replacements: 800
Total Samples: 905
Nested Sampling ln(Z): -43.400549
Importance Nested Sampling ln(Z): -1.489110 +/- 0.071509
Acceptance Rate: 0.850851
Replacements: 850
Total Samples: 999
Nested Sampling ln(Z): -24.490757
Importance Nested Sampling ln(Z): -1.480349 +/- 0.068075
Acceptance Rate: 0.811542
Replacements: 900
Total Samples: 1109
Nested Sampling ln(Z): -15.277327
Importance Nested Sampling ln(Z): -3.650556 +/- 0.064788
Acceptance Rate: 0.750395
Replacements: 950
Total Samples: 1266
Nested Sampling ln(Z): -11.972138
Importance Nested Sampling ln(Z): -4.355198 +/- 0.058615
Acceptance Rate: 0.675219
Replacements: 1000
Total Samples: 1481
Nested Sampling ln(Z): -10.036362
Importance Nested Sampling ln(Z): -4.818506 +/- 0.053064
Acceptance Rate: 0.629874
Replacements: 1050
Total Samples: 1667
Nested Sampling ln(Z): -8.574231
Importance Nested Sampling ln(Z): -4.967739 +/- 0.048733
Acceptance Rate: 0.584795
Replacements: 1100
Total Samples: 1881
Nested Sampling ln(Z): -7.308692
Importance Nested Sampling ln(Z): -5.089997 +/- 0.046080
Acceptance Rate: 0.553950
Replacements: 1150
Total Samples: 2076
Nested Sampling ln(Z): -6.403580
Importance Nested Sampling ln(Z): -5.168678 +/- 0.044278
Acceptance Rate: 0.525855
Replacements: 1200
Total Samples: 2282
Nested Sampling ln(Z): -5.669126
Importance Nested Sampling ln(Z): -5.222377 +/- 0.043105
Acceptance Rate: 0.498206
Replacements: 1250
Total Samples: 2509
Nested Sampling ln(Z): -5.049320
Importance Nested Sampling ln(Z): -5.276605 +/- 0.041752
Acceptance Rate: 0.471014
Replacements: 1300
Total Samples: 2760
Nested Sampling ln(Z): -4.555645
Importance Nested Sampling ln(Z): -5.347137 +/- 0.041259
Acceptance Rate: 0.442768
Replacements: 1350
Total Samples: 3049
Nested Sampling ln(Z): -4.118150
Importance Nested Sampling ln(Z): -5.409999 +/- 0.041079
Acceptance Rate: 0.430504
Replacements: 1400
Total Samples: 3252
Nested Sampling ln(Z): -3.737626
Importance Nested Sampling ln(Z): -5.420068 +/- 0.040312
Acceptance Rate: 0.411581
Replacements: 1450
Total Samples: 3523
Nested Sampling ln(Z): -3.411136
Importance Nested Sampling ln(Z): -5.460463 +/- 0.040277
Acceptance Rate: 0.397772
Replacements: 1500
Total Samples: 3771
Nested Sampling ln(Z): -3.147723
Importance Nested Sampling ln(Z): -5.484940 +/- 0.040107
Acceptance Rate: 0.383094
Replacements: 1550
Total Samples: 4046
Nested Sampling ln(Z): -2.929285
Importance Nested Sampling ln(Z): -5.501794 +/- 0.039860
Acceptance Rate: 0.361582
Replacements: 1600
Total Samples: 4425
Nested Sampling ln(Z): -2.743752
Importance Nested Sampling ln(Z): -5.527151 +/- 0.039778
Acceptance Rate: 0.344756
Replacements: 1650
Total Samples: 4786
Nested Sampling ln(Z): -2.583889
Importance Nested Sampling ln(Z): -5.531862 +/- 0.039364
Acceptance Rate: 0.332681
Replacements: 1700
Total Samples: 5110
Nested Sampling ln(Z): -2.448166
Importance Nested Sampling ln(Z): -5.521621 +/- 0.038604
Acceptance Rate: 0.317086
Replacements: 1750
Total Samples: 5519
Nested Sampling ln(Z): -2.331706
Importance Nested Sampling ln(Z): -5.519770 +/- 0.038128
Acceptance Rate: 0.301306
Replacements: 1800
Total Samples: 5974
Nested Sampling ln(Z): -2.230707
Importance Nested Sampling ln(Z): -5.512875 +/- 0.037503
Acceptance Rate: 0.284615
Replacements: 1850
Total Samples: 6500
Nested Sampling ln(Z): -2.143750
Importance Nested Sampling ln(Z): -5.523491 +/- 0.037465
Acceptance Rate: 0.271351
Replacements: 1900
Total Samples: 7002
Nested Sampling ln(Z): -2.067318
Importance Nested Sampling ln(Z): -5.529275 +/- 0.037391
Acceptance Rate: 0.261780
Replacements: 1950
Total Samples: 7449
Nested Sampling ln(Z): -2.000580
Importance Nested Sampling ln(Z): -5.528270 +/- 0.037172
Acceptance Rate: 0.254745
Replacements: 2000
Total Samples: 7851
Nested Sampling ln(Z): -1.942019
Importance Nested Sampling ln(Z): -5.529648 +/- 0.037062
Acceptance Rate: 0.244952
Replacements: 2050
Total Samples: 8369
Nested Sampling ln(Z): -1.890137
Importance Nested Sampling ln(Z): -5.534155 +/- 0.037056
Acceptance Rate: 0.234689
Replacements: 2100
Total Samples: 8948
Nested Sampling ln(Z): -1.844308
Importance Nested Sampling ln(Z): -5.541646 +/- 0.037198
Acceptance Rate: 0.229701
Replacements: 2150
Total Samples: 9360
Nested Sampling ln(Z): -1.803641
Importance Nested Sampling ln(Z): -5.533335 +/- 0.036839
Acceptance Rate: 0.223282
Replacements: 2200
Total Samples: 9853
Nested Sampling ln(Z): -1.767468
Importance Nested Sampling ln(Z): -5.537262 +/- 0.036911
Acceptance Rate: 0.214204
Replacements: 2250
Total Samples: 10504
Nested Sampling ln(Z): -1.735158
Importance Nested Sampling ln(Z): -5.540624 +/- 0.036973
Acceptance Rate: 0.208484
Replacements: 2300
Total Samples: 11032
Nested Sampling ln(Z): -1.706283
Importance Nested Sampling ln(Z): -5.532352 +/- 0.036641
Acceptance Rate: 0.203534
Replacements: 2350
Total Samples: 11546
Nested Sampling ln(Z): -1.680385
Importance Nested Sampling ln(Z): -5.522709 +/- 0.036262
Acceptance Rate: 0.198890
Replacements: 2400
Total Samples: 12067
Nested Sampling ln(Z): -1.657115
Importance Nested Sampling ln(Z): -5.519607 +/- 0.036124
Acceptance Rate: 0.194013
Replacements: 2450
Total Samples: 12628
Nested Sampling ln(Z): -1.636183
Importance Nested Sampling ln(Z): -5.524050 +/- 0.036266
Acceptance Rate: 0.189825
Replacements: 2500
Total Samples: 13170
Nested Sampling ln(Z): -1.617379
Importance Nested Sampling ln(Z): -5.517423 +/- 0.036026
Acceptance Rate: 0.183546
Replacements: 2550
Total Samples: 13893
Nested Sampling ln(Z): -1.600464
Importance Nested Sampling ln(Z): -5.514185 +/- 0.035907
Acceptance Rate: 0.180455
Replacements: 2600
Total Samples: 14408
Nested Sampling ln(Z): -1.585233
Importance Nested Sampling ln(Z): -5.512749 +/- 0.035855
Acceptance Rate: 0.176514
Replacements: 2650
Total Samples: 15013
Nested Sampling ln(Z): -1.571536
Importance Nested Sampling ln(Z): -5.507917 +/- 0.035685
Acceptance Rate: 0.170929
Replacements: 2700
Total Samples: 15796
Nested Sampling ln(Z): -1.559212
Importance Nested Sampling ln(Z): -5.507698 +/- 0.035684
Acceptance Rate: 0.166646
Replacements: 2750
Total Samples: 16502
Nested Sampling ln(Z): -1.548108
Importance Nested Sampling ln(Z): -5.504278 +/- 0.035573
Acceptance Rate: 0.162677
Replacements: 2800
Total Samples: 17212
Nested Sampling ln(Z): -1.538103
Importance Nested Sampling ln(Z): -5.502251 +/- 0.035513
Acceptance Rate: 0.162217
Replacements: 2807
Total Samples: 17304
Nested Sampling ln(Z): -1.536784
Importance Nested Sampling ln(Z): -5.501803 +/- 0.035498
ln(ev)= -1.4446729281324759 +/- 5.6068666796503325E-002
Total Likelihood Evaluations: 17304
Sampling finished. Exiting MultiNest
analysing data from chains/PP-example-bosonic-adm-run.txt
6295.144674062729
Finally, NEoST also includes functionality to perform the first steps of posterior analysis. The first step in this process is to call the PosteriorAnalysis.compute_auxiliary_data() function with the code block below. This function also has a dm boolean parameter (default dm = False) that will compute the ADM admixed data. Note, if one wishes to compute the effect of ADM on the baryonic EoS posterior simply follow everything above, but set dm = False. This will generate as output
a set of files that can subsequently be used with several additional plotting routines included in NEoST, or you can analyse these files on your own. For the following posterior analysis examples we use previously computed high-resolution MultiNest example outputs to avoid problems with too few samples. Note that computing the auxiliary data might take some time.
[6]:
# Compute auxiliary data for posterior analysis
PosteriorAnalysis.compute_auxiliary_data(directory, polytropes_pp, variable_params, static_params, chirp_mass, dm=True, identifier=run_name)
Total number of samples is 1843
sample too small for 69057064623221538816.00
sample too small for 80266305250404122624.00
sample too small for 93295051751504232448.00
sample too small for 108438650691020767232.00
sample too small for 126040390014373543936.00
sample too small for 146499281011163594752.00
sample too small for 170279103465895788544.00
sample too small for 197918919039913820160.00
sample too small for 230045291211449303040.00
sample too small for 267386488786475515904.00
sample too small for 310788994958532935680.00
sample too small for 361236696159908855808.00
sample too small for 419873185694463426560.00
sample too small for 488027687751237173248.00
sample too small for 567245189467959590912.00
sample too small for 659321464105415868416.00
sample too small for 766343779270003916800.00
sample too small for 890738212995494576128.00
sample too small for 1035324650287871295488.00
sample too small for 1203380706845202317312.00
sample too small for 1398716029033563815936.00
sample too small for 1625758654418290475008.00
sample too small for 1889655390550021111808.00
sample too small for 2196388487483154235392.00
sample too small for 2552911248865209352192.00
sample too small for 2967305655753387278336.00
sample too small for 3448965576317909073920.00
sample too small for 4008809714596653301760.00
sample too small for 4659529125617606852608.00
sample too small for 5415874907786789781504.00
sample too small for 6294992594214729023488.00
sample too small for 7316810823268955062272.00
sample too small for 8504493099089720770560.00
sample too small for 9884962882987738791936.00
sample too small for 11489513918974551654400.00
sample too small for 13354519628839080951808.00
sample too small for 15522257657984079364096.00
sample too small for 18041868263579327660032.00
sample too small for 20970468270644872085504.00
sample too small for 24374445848235373232128.00
sample too small for 28330965456892742074368.00
sample too small for 32929717082882972844032.00
sample too small for 38274949412452242030592.00
sample too small for 44487833035949889028096.00
sample too small for 51709207253076462796800.00
sample too small for 60102772746339840163840.00
sample too small for 69858802497152293535744.00
sample too small for 81198455066986041835520.00
sample too small for 94378788020972804898816.00
sample too small for 109698585142804871118848.00
sample too small for 127505129537538600468480.00
sample too small for 148202076161164196184064.00
sample too small for 172258602238619070496768.00
sample too small for 200220043000234507239424.00
sample too small for 232720253837175185997824.00
sample too small for 270495979112483075915776.00
sample too small for 314403553352988674228224.00
sample too small for 365438313419917846642688.00
sample too small for 424757161710978743664640.00
sample too small for 493704791877090665299968.00
sample too small for 573844171562187623497728.00
sample too small for 666991973176637931913216.00
sample too small for 775259755881237128937472.00
sample too small for 901101832332496760471552.00
sample too small for 1047370905276255775490048.00
sample too small for 1217382735210462192861184.00
sample too small for 1414991305062602833395712.00
sample too small for 1644676185783224816893952.00
sample too small for 1911644083338190283341824.00
sample too small for 2221946869059373502562304.00
sample too small for 2582618768973408491274240.00
sample too small for 3001835822040823359340544.00
sample too small for 3489101222050157413007360.00
sample too small for 4055460744666110756913152.00
sample too small for 4713753143127766290399232.00
sample too small for 5478901188794619541848064.00
sample too small for 6368249954112883954548736.00
sample too small for 7401960006507691117641728.00
sample too small for 8603464426478405628723200.00
sample too small for 10000000010000001178533888.00
sample too small for 1929421597814328.25
sample too small for 1970027832061813.25
sample too small for 2011488657271488.25
sample too small for 2053822058999672.50
sample too small for 2097046401323230.50
sample too small for 2141180434805824.25
sample too small for 2186243304631855.50
sample too small for 2232254558911596.75
sample too small for 2279234157161073.50
sample too small for 2327202478960412.00
sample too small for 2376180332794444.50
sample too small for 2426188965079374.50
sample too small for 2477250069379378.50
sample too small for 2529385795817171.50
sample too small for 2582618760682674.50
sample too small for 2636972056243897.50
sample too small for 2692469260764263.50
sample too small for 2749134448730738.00
sample too small for 2806992201297336.00
sample too small for 2866067616948244.00
sample too small for 2926386322385546.50
sample too small for 2987974483645901.50
sample too small for 3050858817451368.50
sample too small for 3115066602798930.00
sample too small for 3180625692794119.00
sample too small for 3247564526733497.00
sample too small for 3315912142441618.50
sample too small for 3385698188867432.00
sample too small for 3456952938945992.50
sample too small for 3529707302730642.50
sample too small for 3603992840801795.00
sample too small for 3679841777957681.00
sample too small for 3757287017193471.50
sample too small for 3836362153974356.50
sample too small for 3917101490809260.50
sample too small for 3999540052131019.50
sample too small for 4083713599489982.50
sample too small for 4169658647067114.50
sample too small for 4257412477513845.50
sample too small for 4347013158125017.50
sample too small for 4438499557352477.50
sample too small for 4531911361665928.00
sample too small for 4627289092768923.00
sample too small for 4724674125176885.00
sample too small for 4824108704165373.00
sample too small for 4925635964095779.00
sample too small for 5029299947127007.00
sample too small for 5135145622320654.00
sample too small for 5243218905148582.00
sample too small for 5353566677410718.00
sample too small for 5466236807572385.00
sample too small for 5581278171529287.00
sample too small for 5698740673809881.00
sample too small for 5818675269223598.00
sample too small for 5941133984965040.00
sample too small for 6066169943182997.00
sample too small for 6193837384024844.00
sample too small for 6324191689165517.00
sample too small for 6457289405832088.00
sample too small for 6593188271333542.00
sample too small for 6731947238107223.00
sample too small for 6873626499291975.00
sample too small for 7018287514839926.00
sample too small for 7165993038177370.00
sample too small for 7316807143427177.00
sample too small for 7470795253203829.00
sample too small for 7628024166993457.00
sample too small for 7788562090131269.00
sample too small for 7952478663388850.00
sample too small for 8119844993184009.00
sample too small for 8290733682426425.00
sample too small for 8465218862012588.00
sample too small for 8643376222983586.00
sample too small for 8825283049359533.00
sample too small for 9011018251665036.00
sample too small for 9200662401160358.00
sample too small for 9394297764793012.00
sample too small for 9592008340884800.00
sample too small for 9793879895569906.00
sample too small for 10000000000000000.00
sample too small for 9772713302804146176.00
sample too small for 11358836325422383104.00
sample too small for 13202418376723152896.00
sample too small for 15345250749730207744.00
sample too small for 17835908401382062080.00
sample too small for 20730851093564043264.00
sample too small for 24095703274071531520.00
sample too small for 28006741711008706560.00
sample too small for 32552624603674001408.00
sample too small for 37836401366994427904.00
sample too small for 43977848649127854080.00
sample too small for 51116185537207795712.00
sample too small for 59413229501990084608.00
sample too small for 69057064623221538816.00
sample too small for 80266305250404122624.00
sample too small for 93295051751504232448.00
sample too small for 108438650691020767232.00
sample too small for 126040390014373543936.00
sample too small for 146499281011163594752.00
sample too small for 170279103465895788544.00
sample too small for 197918919039913820160.00
sample too small for 230045291211449303040.00
sample too small for 267386488786475515904.00
sample too small for 310788994958532935680.00
sample too small for 361236696159908855808.00
sample too small for 419873185694463426560.00
sample too small for 488027687751237173248.00
sample too small for 567245189467959590912.00
sample too small for 659321464105415868416.00
sample too small for 766343779270003916800.00
sample too small for 890738212995494576128.00
sample too small for 1035324650287871295488.00
sample too small for 1203380706845202317312.00
sample too small for 1398716029033563815936.00
sample too small for 1625758654418290475008.00
sample too small for 1889655390550021111808.00
sample too small for 2196388487483154235392.00
sample too small for 2552911248865209352192.00
sample too small for 2967305655753387278336.00
sample too small for 3448965576317909073920.00
sample too small for 4008809714596653301760.00
sample too small for 4659529125617606852608.00
sample too small for 5415874907786789781504.00
sample too small for 6294992594214729023488.00
sample too small for 7316810823268955062272.00
sample too small for 8504493099089720770560.00
sample too small for 9884962882987738791936.00
sample too small for 11489513918974551654400.00
sample too small for 13354519628839080951808.00
sample too small for 15522257657984079364096.00
sample too small for 18041868263579327660032.00
sample too small for 20970468270644872085504.00
sample too small for 24374445848235373232128.00
sample too small for 28330965456892742074368.00
sample too small for 32929717082882972844032.00
sample too small for 38274949412452242030592.00
sample too small for 44487833035949889028096.00
sample too small for 51709207253076462796800.00
sample too small for 60102772746339840163840.00
sample too small for 69858802497152293535744.00
sample too small for 81198455066986041835520.00
sample too small for 94378788020972804898816.00
sample too small for 109698585142804871118848.00
sample too small for 127505129537538600468480.00
sample too small for 148202076161164196184064.00
sample too small for 172258602238619070496768.00
sample too small for 200220043000234507239424.00
sample too small for 232720253837175185997824.00
sample too small for 270495979112483075915776.00
sample too small for 314403553352988674228224.00
sample too small for 365438313419917846642688.00
sample too small for 424757161710978743664640.00
sample too small for 493704791877090665299968.00
sample too small for 573844171562187623497728.00
sample too small for 666991973176637931913216.00
sample too small for 775259755881237128937472.00
sample too small for 901101832332496760471552.00
sample too small for 1047370905276255775490048.00
sample too small for 1217382735210462192861184.00
sample too small for 1414991305062602833395712.00
sample too small for 1644676185783224816893952.00
sample too small for 1911644083338190283341824.00
sample too small for 2221946869059373502562304.00
sample too small for 2582618768973408491274240.00
sample too small for 3001835822040823359340544.00
sample too small for 3489101222050157413007360.00
sample too small for 4055460744666110756913152.00
sample too small for 4713753143127766290399232.00
sample too small for 5478901188794619541848064.00
sample too small for 6368249954112883954548736.00
sample too small for 7401960006507691117641728.00
sample too small for 8603464426478405628723200.00
sample too small for 10000000010000001178533888.00
sample too small for 2.32
sample too small for 2.33
sample too small for 2.34
sample too small for 2.36
sample too small for 2.37
sample too small for 2.38
sample too small for 2.40
sample too small for 2.41
sample too small for 2.43
sample too small for 2.44
sample too small for 2.45
sample too small for 2.47
sample too small for 2.48
sample too small for 2.49
sample too small for 2.51
sample too small for 2.52
sample too small for 2.53
sample too small for 2.55
sample too small for 2.56
sample too small for 2.57
sample too small for 2.59
sample too small for 2.60
sample too small for 2.62
sample too small for 2.63
sample too small for 2.64
sample too small for 2.66
sample too small for 2.67
sample too small for 2.68
sample too small for 2.70
sample too small for 2.71
sample too small for 2.72
sample too small for 2.74
sample too small for 2.75
sample too small for 2.76
sample too small for 2.78
sample too small for 2.79
sample too small for 2.81
sample too small for 2.82
sample too small for 2.83
sample too small for 2.85
sample too small for 2.86
sample too small for 2.87
sample too small for 2.89
sample too small for 2.90
These following plotting routines will do the follwoing:
Create a cornerplot of all the parameters you have included in the
variable_paramsdictionary and requiresdmboolean parameter so that it can take the log_10 of the mchi and g_chi_over_mphi parameters since they span several orders of magnitude.This will plot the data you have used to define the likelihood. So these are the masses and radii of the neutron stars that have been included in the analysis. Note that this will also plot the masses and radii of any gravitational wave events included in the data.
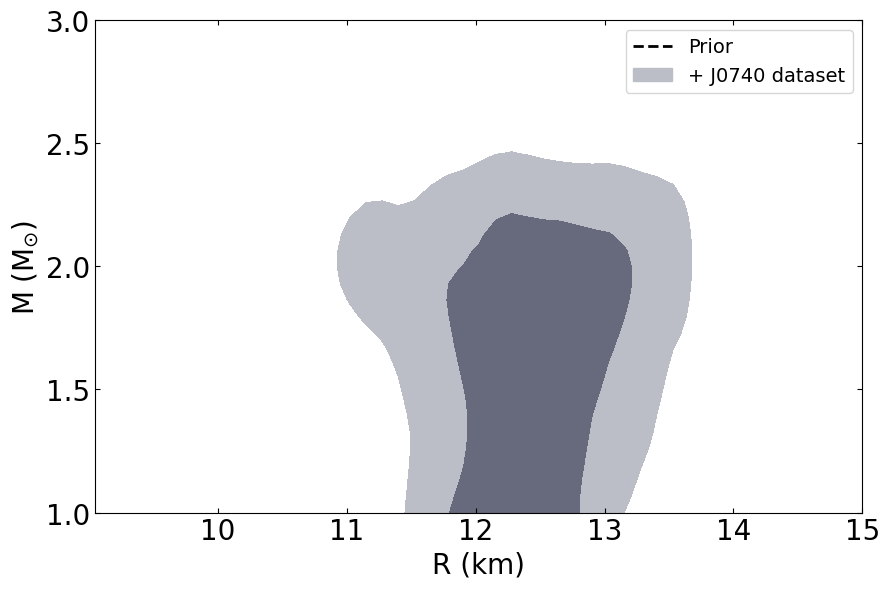
This routine will plot the posterior on the mass-radius relationship of neutron stars according to the inference process, the
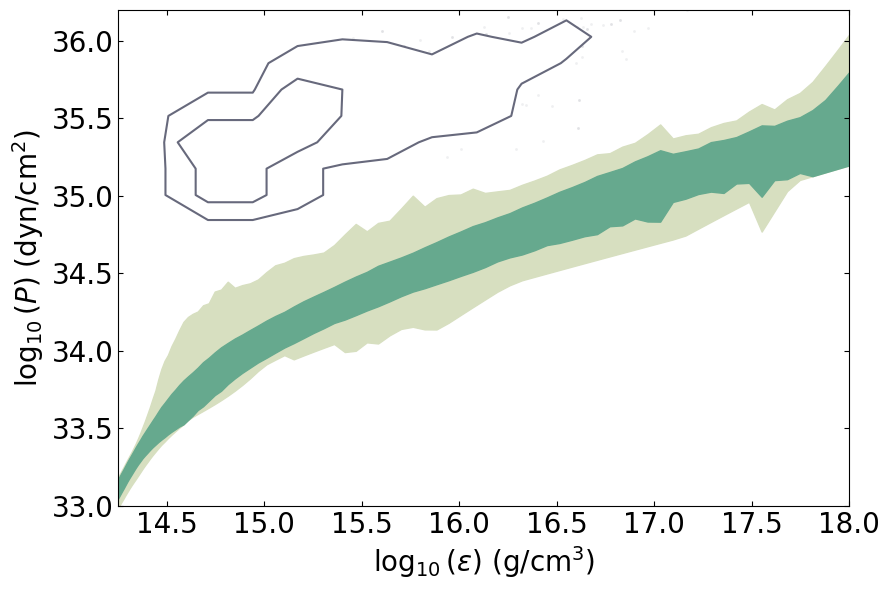
label_nameparameter will be the label used in the legend. Ifdm = True, it will plot the posteriors in which ADM halos are not included.This routine will plot the posterior on the equation of state itself.
[7]:
PosteriorAnalysis.cornerplot(directory, variable_params, dm=True, identifier=run_name)

[8]:
PosteriorAnalysis.mass_radius_posterior_plot(directory, identifier=run_name)
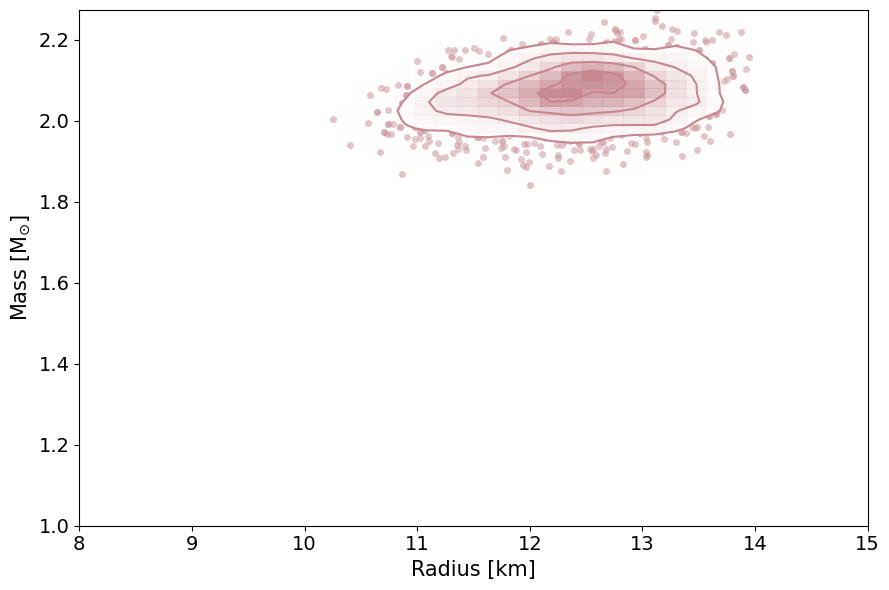
[9]:
PosteriorAnalysis.mass_radius_prior_predictive_plot(directory, variable_params, identifier=run_name, label_name='+ J0740 dataset')
[6]:
PosteriorAnalysis.eos_posterior_plot(directory, variable_params, dm=True, identifier=run_name)
[7]:
pressures = np.load(f'{directory}/{run_name}pressures.npy')
pressures_b = np.load(f'{directory}/{run_name}pressures_baryon.npy')